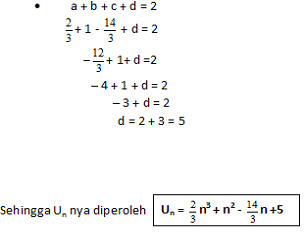Kalo kita resapi (cielah resapi lebay banget ya,….) teka-teki di atas, kan yang di bahas umur Ibu ma anaknya ko pertanyaanya malah “apa yang dilakukan Ayahnya” aneh kan???? Pasti dari sebagian kita akan menjawab “Ya terserah Ayahnya mau ngapain ke, ngapain juga kita pusing-pusing mikrin ayah orang” bener ga??? Hehehhehe…..
Jawaban tadi ada benernya juga,.. kita kan ga tau ayahnya lagi apa, soalnya kita waktu itu ga bersama “Ayah” tersebut,… jadi bebas-bebas aja mau jawab apa,…
Tapi kalo kita pandang dari sisi matematikanya kita tidak akan cuma jawab doang,.. pasti umur dari Ibu dan anaknya ada hubunganya dengan pekerjaan yang sedang dikerjakan ayahnya di saat itu..
Dan setelah kita mengerjakan hitungan aljabar untuk mencari umur si Ibu dan anaknya, baru dah kita tau yang di kerjakan ayahnya saat itu,….
Pingin tau jawabanya??? Tunggu postingan selanjutnya ya,…… hehehhe







 01.16
01.16
 Unknown
Unknown


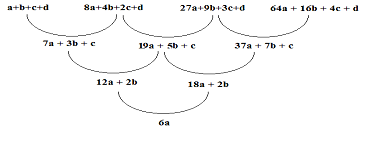
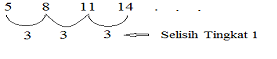 Bentuk umum barisan tersebut adalah
Bentuk umum barisan tersebut adalah