Barisan Berderajat

1. Barisan berderajat satu
Barisan berderajat satu yaitu barisan yang mempunyai selisih tetap pada tingkat pertama penyelidikan

1. Contoh: 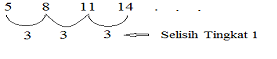Bentuk umum barisan tersebut adalah
   U_n = an + b
   U₁ = a + b
   U₂= 2a + b
   Dst….
   Sehingga di peroleh:
   
   Untuk barisan 5, 8, 11, 14, … diperoleh a = 3. Nilai b diperoleh dengan mensubstitusi ke U₁ sehingga diperoleh
   
   Gimana untuk untuk berderajat dua dan seterusnya?????
   
   
   2. Barisan berderajat dua
   Barisan berderajat dua yaitu barisan yang memiliki selisih tetap pada tinggkat ke dua penyelidikan
2. Contoh

Bentuk umum barisan tersebut adalah
U_n = an² + bn + c
U₁ = a(1)² + b(1)+c = a + b + c
U₂ = a(2)² + b(2)+c = 4a + 2b + c
U₃ = a(3)² + b(3)+c = 9a +3 b + c
U₄ = a(4)² + b(4)+c = 16a +4 b + c
dst,……
Sehingga diperoleh

Untuk rums suku ke-n dari barisan 5, 8, 13, 20, 29,…
Diperoleh:

3. Barisan berderajat Tiga

Barisan berderajat dua yaitu barisan yang memiliki selisih tetap pada tinggkat ke dua penyelidikan

Contoh

Bentuk umum barisan tersebut adalah
U_n = an³ + bn² + cn + d
U₁ = a(1)³ + b(1)² + c(1) + d = a + b + c + d
U₂ = a(2)³ + b(2)² + c(2) + d = 8a + 4b + 2c + d
U₃ = a(3)³ + b(3)² + c(3) + d = 27a + 9b + 3c + d
U₄ = a(4)³ + b(4)² + c(4) + d = 64a + 16b + 4c + d
dst,……
Sehingga diperoleh..

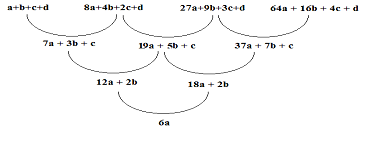
Untuk barisan di atas diperoleh


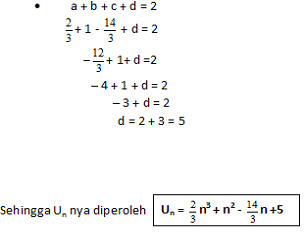
Nah itulah barisan berderajat 1, 2, dan 3. Untuk yang berderajat lebih dari 3 ilustrasinya sama dengan yang kita bahas tadi.
Semoga postingan ini bermanfaat,……!!

Posted in: Artikel,Math